Today at Interbike TrainerRoad demo’d their upcoming desktop app refresh. The goal of the app update, aside from looking prettier, is to lay a better foundation for new features going forward. And to a large degree to just make finding features easier.
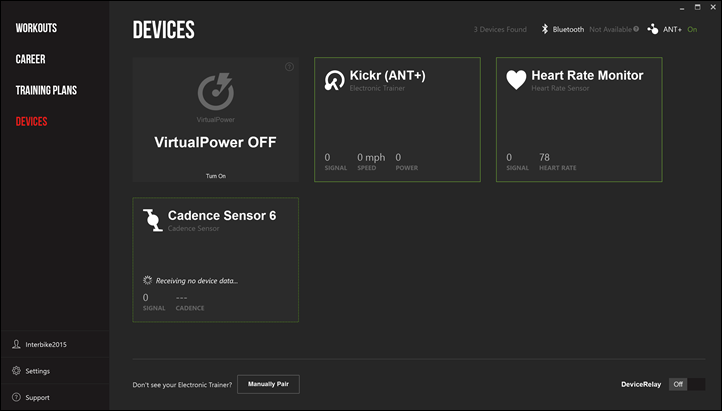
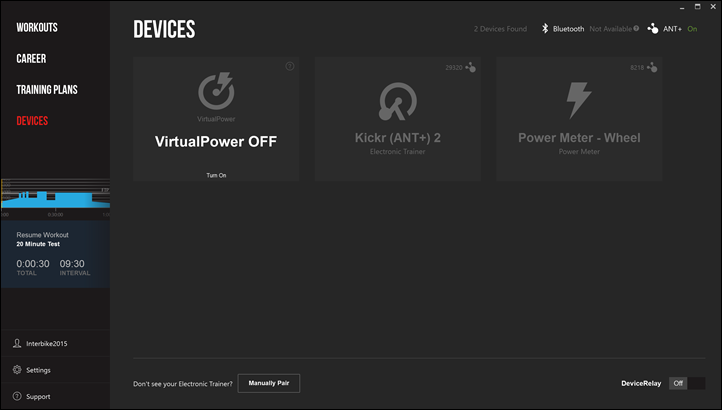
To start, you’ll see the Devices page now looks drastically different. Rather than showing you a list of one million potential device types to search for (like they do today), you’ll just see those devices/sensors that you’ve scanned and successfully found (ANT+ or Bluetooth Smart):
You’ve still got support for products like CompuTrainer, and my favorite – DeviceRelay (allows you to retransmit out your Virtual Power or CompuTrainer as ANT+).
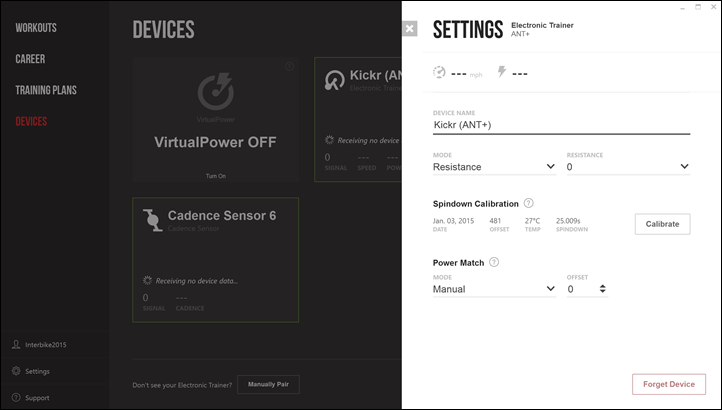
Once you connect to a sensor you can look at the settings and do all the usual goodness like calibration and Power Match (to utilize a power meter to drive the trainer).
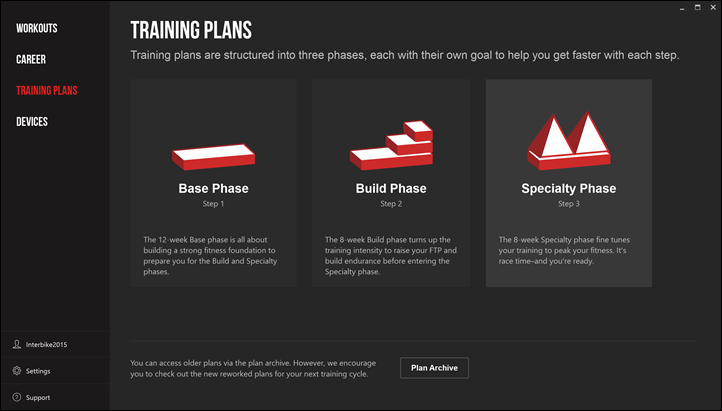
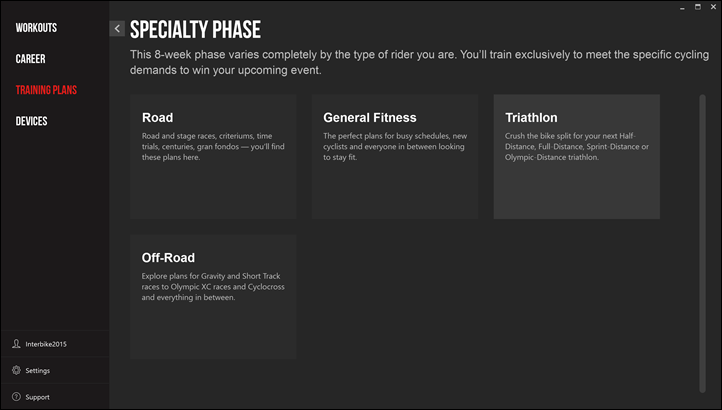
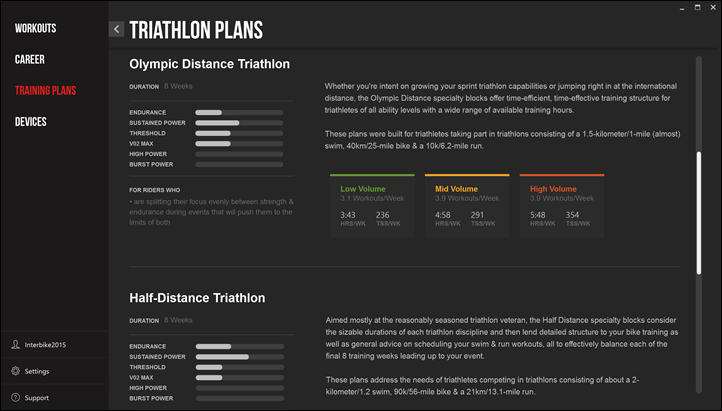
Next, they’ve made the training plans section a bit more clear. TrainerRoad introduced the plans a while back, but this makes it easier to actually figure out how to use them and where to start. Essentially they’ve got three chunks (just like in real life). These phases follow along how you’d approach a season and target a given race. For example, you’ll start with the 12-week base phase, then the 8 week build phase, followed by your specialty phase. The specialty phase is targeted towards a given race or situation (i.e. road vs triathlon)
For example, here’s the specialty phase:
And then into a specific triathlon plan, for example:
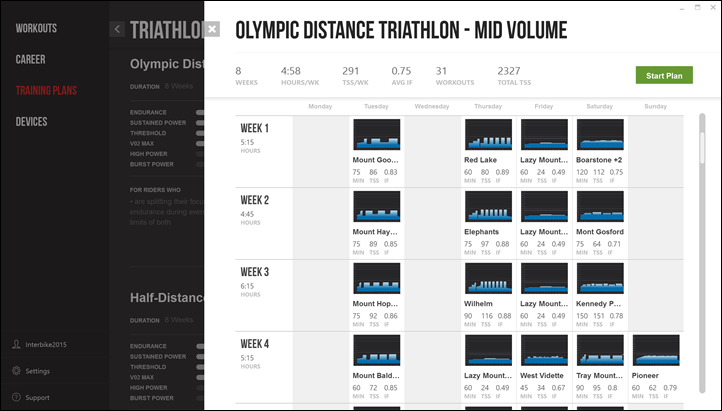
And even then, an Olympic Distance triathlon plan:
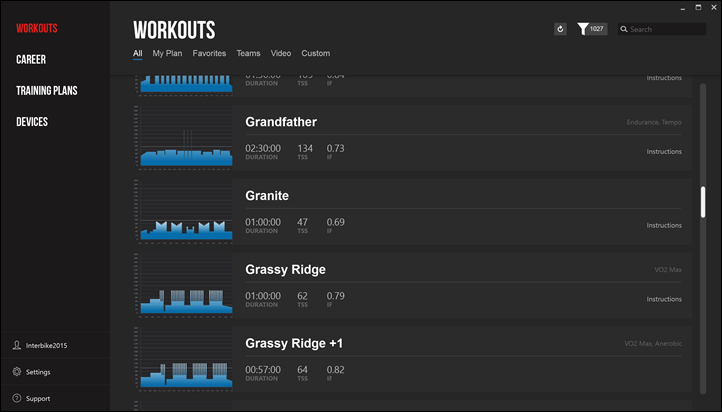
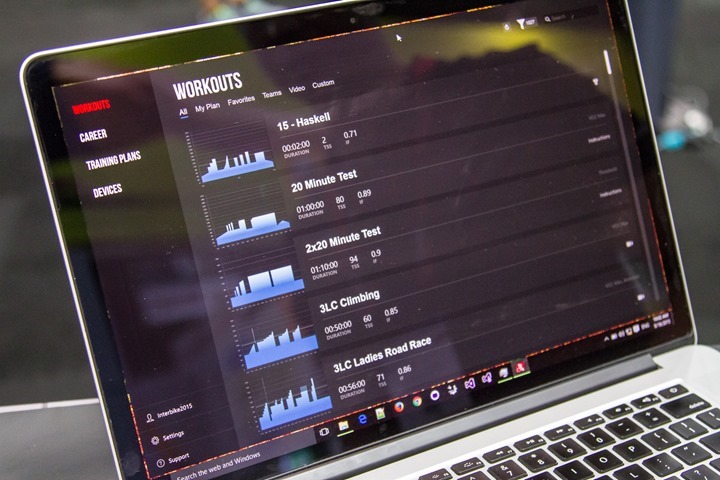
All of this matters when you get into actually working out (overrated in my opinion). Necessary I suppose. So you’ll go into Workouts and pick your poison.
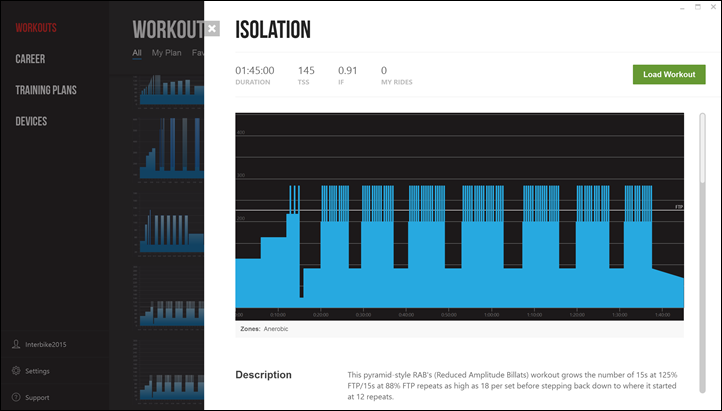
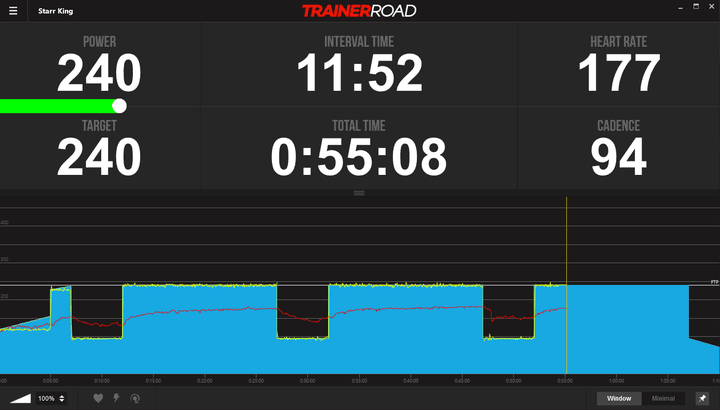
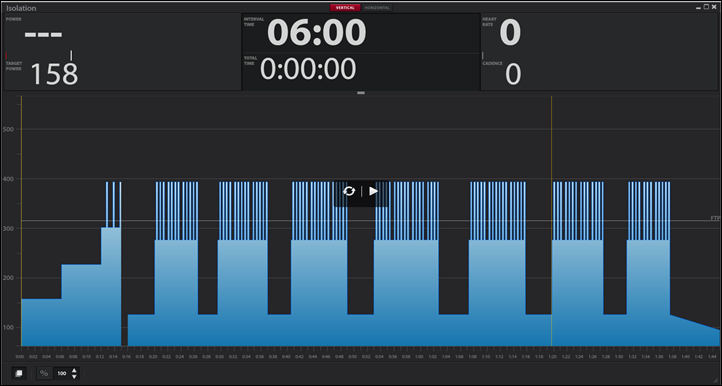
In this case the workout called Isolation, which features the always fun 15s repeats.
Once you load the workout, you’ll see the new look and feel to things:
Compare this to previous:
You’ve also got a few more options when it comes to settings mid-workout, where you’ll see the actual workout window will shrink down to the left-side, allowing you to tweak things as you see fit.
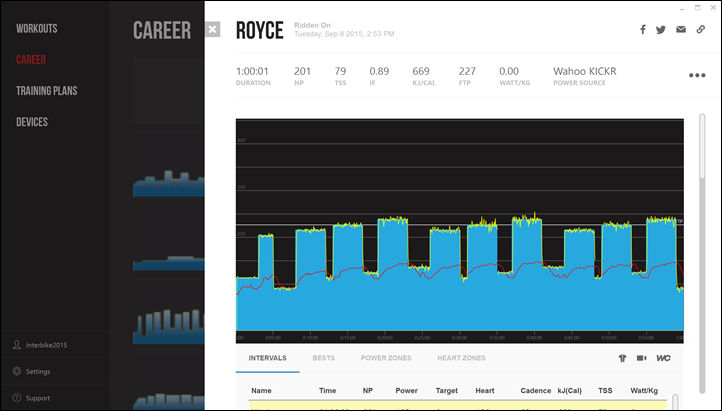
After the ride you’ll get display of the data in a fairly similar format to before, just in a newly styled page:
So when’s all this new jazz available? TrainerRoad will begin an open beta by the end of the month, allowing people to try it for themselves. There are some features that’ll be layered in as the beta progresses. For example some of the social sharing pieces aren’t yet there today, but will be by time the beta finishes.
And last but not least, earlier this week TrainerRoad announced that they’ve begun Android development efforts. This would bring their mobile app onto the Android platform (it’s already on iOS). When I asked about timelines, they weren’t at the point of being able to establish those. In other words, don’t expect it final by next month or anything – it’s a wee bit further out than that. Still, you can sign-up on their Android updates list here. There are no plans for Windows Phone/Windows 10 Mobile support (market share is simply too small for them).
Speaking of platforms – one has to wonder how far away they might be from looking at Apple TV (now with apps via tvOS). Given the Bluetooth Smart support there, it might make for the ideal lightweight trainer to TV platform depending on how much connectivity Apple is allowing there. And, now that I’ve decided to stir that pot…I’ll call this post done.
—
With that, thanks for reading! If you’re looking to burn a bit of time, here’s all my Interbike 2015 posts!
FOUND THIS POST USEFUL? SUPPORT THE SITE!
Hopefully, you found this post useful. The website is really a labor of love, so please consider becoming a DC RAINMAKER Supporter. This gets you an ad-free experience, and access to our (mostly) bi-monthly behind-the-scenes video series of “Shed Talkin’”.
Support DCRainMaker - Shop on Amazon
Otherwise, perhaps consider using the below link if shopping on Amazon. As an Amazon Associate, I earn from qualifying purchases. It doesn’t cost you anything extra, but your purchases help support this website a lot. It could simply be buying toilet paper, or this pizza oven we use and love.






















Did you get a chance to try the workout editor Ray? This is (in my mind) one of the big weaknesses of TrainerRoad. Big enough that I switched to PerfPro to get fast workout setup. So I’m hoping they’ve made it a lot easier to use in this new version.
I did not. Perhaps I’ll swing back down again tomorrow morning and poke.
Thanks for the PerfPro tip. I NEEDED a program who can do the analysis for me + TR type workouts.
We don’t have a new Workout Creator to show right now. It’s on the short list after we launch our new software. We’ve heard the requests of people who want to enter in a more “excel” like format for their workout.
For those unfamiliar with our workout creator we have a great youtube video tutorial that shows how to use it and what you can do with it: link to youtube.com
On the workout editor, I would love to see something where I can import a course, and have it build a workout for it. For example, grab a copy of the route of a race and then you can take practice runs at the course on a trainer.
Yes flobble
If I want a quick HIIT session I stick on the Wahoo Fitness App in Erg Mode (iPad Mini) and cycle (Wahoo Kickr) at about 60% FTP sticking in the HIITs at regular intervals. I can make them higher or lower, longer or shorter or extend the rest period all at a touch. Very flexible.
You can create a route on https://www.bestbikesplit.com and set your projected time on the route. Then export a workout that can be imported into Trainerroad.
I agree! Best bike split actually just built something like this. I think you can use it on their free version. Check it out here: link to bestbikesplit.com.
You can grab an MRC file from them and drop it in the TrainerRoad Workout Creator.
OH man, as an engineer that LOVES spreadsheets, PP just seems archaic and dreadfully arduous to me when compared to workout creator. I do wish in workout creator that I could snap workout intervals to the closest end point on another interval so I didn’t have to go in and tweak durations if I don’t line it up juuuuuuust right.
Andrew
That’s a good suggestion andrew. We plan on moving the WC to the web and adding features like the snapping of intervals :).
Any screenshots in the horizontal mode Ray? (Gotta have a movie/show going)
The app totally has “horizontal” mode! :) I too love watching TV/Movies while working out :).
But does the horizontal mode look different? Can you share a screenshot of the updated horizontal mode?
The right graph is slightly different. It shows how far you are completing the current interval (like the iOS app). It’s really cool.
Sorry, I don’t have a screenshot of horizontal with data in it at the moment. All will be revealed in just a few short weeks :).
Ive actually found just of a few days ago on the imac the horizontal mode is no longer working so i cannot play a movje and see the workout across the bottom. Only option i have is to cycle and not see what the workout is doing and watch the movie…. or not watch a movie, listen to music and see the workout
Tr is a bit glitchy lately, having a few problems, hopefully support team can help
Yikes, sorry to hear about the troubles! If you’re on the new beta version of our Mac app, the ability to place TR in horizontal mode in front of a full-screen video is not available yet. This, among other features, are to be trickled in as we move further in the beta testing process. In the meantime, you’ll have to manually re-size your Youtube window and place TR beneath/on-top of that — sorry for the hassle.
This feature is still be working on the legacy version of the app. If you’re running the old version of the Mac app (legacy), then this could have to do with the browser you’re using. If you think you’re on the older version of the app, or you’re not sure, shoot an email over to support@trainerroad.com and we’ll be happy to take a look. We’d also like to see what’s up with any other concerns you were having.
In any case, we’ll look forward to hashing it out over with support. Thanks Simon!
The indoor market is getting white-hot with options to choose from. This is awesome.
If they produce a Win10 native version of the desktop app, then (at least in theory) it should run on Xbox One and WP10 devices. BT Smart support might still be an issue though.
This is what people need to highlight more, the shared code of the Windows 10 environment. I’m not a developer or anything, but in theory, if they developed the program for Windows 10 on desktop, then porting it to phones, Xbox and Hololens should be fairly simple.
Specs requirements for PCs to run trainer software always seem really high, but an Xbox One would be able to handle it easy enough, and it’s much easier to assure compatibility when everything is standardised! I’m fairly sure that the Windows 10 upgrade on Xbox One will allow greater scope for USB accessories, i.e. required Bluetooth/ANT+ support. Here’s hoping, anyway!
It looks prettier! Honestly all I use is Sufferfest videos on TR though.
As an aside, do you/anyone else have the disappointing experience of short sprints on the KICKR when using something like TR? It takes ERG mode a good 5-10 seconds to figure out how much resistance to match the target power, and by then it’s basically over. Unrelated to TR, really.
I do actually hear from folks noting the same thing with the TR/KICKR combo specifically on short intervals taking too long. I don’t hear it from folks using the default app (such as myself). Perhaps they can chime in on why there’s a bit longer delay.
Wait, what default app, Ray? The Wahoo app? I don’t know how you are simulating intervals with that.
Yes, the default app. I use wattage numbers, so I simply tap the first column down (i.e. from 300w to 100w). Simple!
Hey Tedder,
We’ve recently put in an update where we tell the Kickr to start an interval two seconds before it starts, that seems to make it so the change happens right when the interval starts.
As far as 5-10 seconds that’s no good! On our side we just tell the kickr “Go to 200 watts” and it responds with “ok” and then it does it’s thing.
One thing that we have noticed is that a lot of people drop/change their cadence when an interval starts. When that happens, the Kickr might take a little longer to lock in since it’s trying to compensate for a cadence and power change.
This new app also has a brand new device layer in it. Before we used a third party layer for some our platforms and a custom on for another. We’ve taken all the stuff we’ve learned over the last four years and made a really outstanding device layer with lots and lots of automated tests to make sure everything performs as well as it can.
If you still experience the Kickr not locking in after you try the new beta please email us and let us know. You can email me directly at nate@trainerroad.com or send it to support@trainerroad.com.
Nate- fantastic! I’ll contact you personally so you can see profiles of intervals like that. As an OSX/Android person all progress is good :)
The Wahoo Kickr takes a few seconds to adjust to a new wattage whatever app your’e using. I thought this was a feature, because if you immediately went to a much higher wattage it would be like hitting a brick wall
As there is a new device layer, do you have contact with Tacx about controlling their trainers over Bluetooth? I know you both support the ANT+ version but adding an extra (very cheap) piece of hardware is a little stupid when not needed (Tacx controls their products over bluetooth on android so it’s in there)
We’re talking to Tacx about this today. I’m fairly confident that we’ll be able to control Tacx trainers over Bluetooth this winter. No promises, but I think it can happen. Right now the ball is in their court, but they have expressed interest.
Thanks Nate for the reply and reading all the questions and answering them!
I hope everything works out great with Tacx.
When the talks are over could you give the result? a Go (with no timeline) or a No Go.
In October a Tacx smart will be standing in my garage, now i’m looking at all the training software options. Best would be a tablet version but for the moment a PC would fit.
Once think I have found is with short sprints, if I’m in the small ring (34)and spinning at a high cadence (95-105) before the interval, when it goes to the higher power, kicker or TR (I don’t know how the magic happens) has trouble getting up to that high effort with that high cadence. When I’m on the big ring (50) it doesn’t seem to happen as much although sometimes it does. Slowing my cadence before the interval hits seems to help this the most.
Hey Bart. I messed up and we’re actually meeting Tacx tomorrow at noon. I’ll have some time tomorrow evening and I’ll post an update here :).
Nate, thanks for being so active here. it’s great to see you answering to a lot of questions. Any update on the Tacx meeting?
In my discussions with Tacx this morning via e-mail (Saturday), Nate and his crew – along with other apps that request it, will be given access this upcoming week over BLE. :)
yay, thanks ray!
Ray is correct, that’s what Tacx told us too! Hurray!
Any Tacx trainer with “Smart” in the name should be able to connect to TR via ANT or BT once integrations are complete. Some older “Smart” trainers might need to update their firmware via an Tacx Mobile Utility.
Will the Companion App on desktop still be supported?
We have 3 TR subs in the household and train with 2 side by side on a laptop and the third on an iPad.
Works awesome!
We won’t have the companion app at first launch :(. We haven’t figured out where that fits in terms of priority. It’s not used very much. I’ll bring it up to the team when I get back to Reno.
Thanks for the reply Nate. Will I be able to continue using the existing Companion App once I’ve upgraded the main app?
If not can you opt not to upgrade?
I guess not many households have three crazy fools all training at the same time every other night, but it saves me having to have two laptops so the Companion App works perfect.
Yes! You’ll still be able to use the old app at the same time as the new app. So in a way you’d have companion…one would just be the old version and one would be the new version. You’d also have to push “play” on both or start both via cadence.
You must have a very fit house if three of you are consistently getting on the trainer. Kudos to you!
Perfect, thanks Nate.
That’s how it works now, we both just start to pedal (me and 15 yr old son) when ready to start the set. Wife uses the Ipad for her set, and chooses the music :-(
Good to hear we can carry on using the Companion App. We use the Time Crunch plans to fit in 3 x 30 min sessions per week as we run, swim and actually ride the bike outside too ;-). We don’t watch much TV in our house………..
Kudos to you for answering every question, awesome work again and pass on my thanks to the guys and girls back at base.
Ken S
Newcastle upon Tyne
England, GB
Hi Nate,
Good to know we will be able to launch the old app and the new one.
To add grist to your mill:
My girlfriend and I are planning to train together this winter. So, a few weeks ago I dug into that and was disappointed to learn that TR only supports one user at a time. Fortunately I discovered the Companion App.
If you don’t support it anymore, maybe the new app could support multi-users… e.g: While doing the same workout, it would be nice to have both power curves with different shades (maybe HR/cadence too) on the same graph on our TV (laptop + hdmi out). It seems doable since workout are based on % of power.
Regards,
Romain
Looking forward to a fresh face to go with my suffering thus winter :-) and I never knew about the plans section!!! That’ll be really useful as I’m doing my first Tri next year.
any updates on being able to export training plans into my email calendar? Like how you can publish your training calendar on Garmin Connect and import into your calendar? Helps to schedule workouts around annoying things like work meetings…..
This! From a user perspective all that should be required is picking a training plan and a start date and then the website should generate a custom iCal-feed for you.
After our platform refresh, calendar will be our next big initiative :).
Would love to have that feature!!!
Would love for them to add in a transparency option when running in horizontal mode. The solid black provides contrast for the information on the banner but removes too much of the movie from your view.
That’s a fantastic idea!! Just sent this to the team.
Have they fixed the issue where when you load up a sufferfest video, if you go into full screen it only shows a quarter of the video?
That’s a limitation of the new way AIR handles video on newer versions of OSX. :(
We’re ditching AIR in favor of native code. The short answer is “YES”, it will fix that. Video support will be much smoother since we’ll be accessing the GPU.
The work around for that full screen video issue is to just stretch the window so it takes up the full screen. Sorry about that :(.
Great news, thanks for letting us know.
When will you release a native app?
Our beta on Windows released in two weeks is written and wpf and c#.
That’s a native app for Windows :). We previously used air as a middle layer
Is it safe to assume the native app would have less cpu requirements than the air middle layer version?
Not that I specifically have issues with TR, but on an older netbook class device I seem to have some minor issues at times.
Yes. Our new app takes less memory. I haven’t looked at CPU yet but we’re really not doing any crazy stuff while you’re working out. On a really old computer it might just take longer for the app to launch since he has to load stuff in memory.
FYI, the new desktop app won’t work on Windows XP. XP users can still use our legacy AIR app.
What .Net version have you targeted? I.e. will it run on my XP netbook that I currently have to use because you’re not supporting Android yet? ;)
When it comes to video
Is there any chance you might look at doing something for people with Dual screens?
I really like the full sized normal workout screen – easy to read what you are doing, what is coming up, and how long to go.
I also like the Sufferfest videos. As I run TR on the laptop, it would be nice to have the video
on the TV screen, and a normal workout graph on the smaller screen – Anychance this might become an ability in the next version of the app?
It won’t support XP because we’re supporting a version of .NET that XP doesn’t support. I forget which version off the top off my head. The legacy app will still be available for Windows XP after we get the new app out.
We’ll try to get Android out as fast as possible so you can enjoy the new hotness on your Android Phone/Tablet :).
Thanks for the reply! .Net 4.0 was the last version that is supported on XP. Very much looking forward to the Android app!
hell yes – flash is dead!!
Hi,
I like the look of the update and will certainly be checking it out in the next month or so when the turbo reappears for the winter and I reactivate my subscription.
Do you know if TrainerRoad has any plans to introduce a pedal smoothness/efficiency metrics (e.g. like the real-time polar graph from Wattbike)?
For example, some of the workouts include specific drills and I’d find it very useful to be able to visualise the difference that changes to my pedaling style can make…plus having a graph to look at always helps to focus on keeping the correct form.
I guess something like this might require use of an actual power meter rather than virtual power but anything that helps to stop me stomping would be great!
We talk about that all the time, but it’s always been a third tier feature in our minds. Doing pedal efficiency drills will help the time go by more quickly during an interval, but it’s really not at the core of making a rider faster.
So right now, a higher priority feature in our minds is the ability for everyone to find the appropriate training plan for them and track against it. Another example would be Android support. There always seems to be something more core to our offering then pedal efficiency so that’s why it hasn’t gotten done yet.
A lot of people don’t know this, but the top riders in the world don’t have a smooth pedal stroke. They are very quad dominant. There are some great studies out there that show this.
Thanks for the reply Nate
Any plans to make it user selectable which sensor to use for each metric? I want to for example display power values from my KICKR but still pull cadence from Stages Power. Last I checked this was not possible in the iOS app, if the Stages Power was connected the power values would always come from it and not the KICKR.
We removed the feature to let a power meter just act as a cadence sensor when we added power match. We should probably add back a check box to do that.
In general, that’s the only request we get asking to choose the “source” we should take from which device. Our automatic choosing of device speed/cadence/power/heart seems to work really well outside the case of someone with a Kickr and a PM and wanting to just use their PM as a cadence sensor.
Hi Nate,
here is an example: link to cyclus2.com
The Cyclus2 can manage power resistance along a sinus wave.
In some situations this is a much better way than to increase or decrease the power in steps!
Ah, so you mean you want to create workouts with curves rather than just lines. You can do multiple little ramps to simulate a sine wave for training, but we don’t have what you’re asking for specifically right now.
When we revamp our workout creator we’ll keep this in mind.
Thanks Nate, a sinusoidal load, sinus-shape or sine wave “classical latin or english” ;-) has many advantages over simple ramps. Think about going from 150 to 450 Watts in very little time and steps (lets say 1min) would mean you have to layout a lot of single ramps.
Ray, If you are in contact to the TrainerRoad team, please ask them if it is possible to integrate a kind of sinus wave training like cyclus2 can do, were the power rises or falls following a sinus curve…
Hi Einundsiebzig,
Nate from TrainerRoad here. I’m not sure what you’re referring to. Can you link me to an example?
he probably means “sine” wave, rather than step increase in power. either that- or he wants to control power with his nose.
When is the trainer software list review coming?
Nate, thanks for chiming in here so much (and Ray, thanks for accidentally providing a convenient forum). Love TR, but I do have one request that I’ve never bothered to submit. It would be *great* to be able to disable the overlay “instructions” either completely or on a case-by-case basis. There are plenty of times when I’m watching TV in horizontal mode and doing something simple I’ve done many times and really, really want the instructions to go away.
Richard, can’t you already do this (entirely)?
See “Profile” tab on the App — “hide text during workout”
I think that is what that option does?
As Tim mentioned this feature is under the profile tab in the current app. In the new windows app, it’s moved to the “settings” section of the app.
It’s also available on iOS.
how about videos on the ipad with trainer road capabilities?
So we’ve actually released this and just not marketed it yet. Right now you can stream videos via dropbox directly to the app.
The only problem is that dropbox has a 2gb limit or so on streaming per day. This isn’t a big deal for most people, but some people like to do back to back workouts and dropbox would cut off the streaming before their workout is over (which is no fun).
Before we wanted to let everyone know about this feature we wanted to add two things:
1) Allow for streaming from other services like Microsoft OneDrive and Google Drive
2) Allow for in app video caching of videos from Dropbox, OneDrive and Drive.
Apple doesn’t actually let us access any of the videos in an iTunes “video” section, so dropbox was the way we initially went.
So unless you have a dropbox pro account, the dropbox streaming might not work very well for you (depending on how much you stream). Once we get a more robust solution out we’ll announce it to all of our subscribers.
Nate,
I have an android app that doesn’t have ant+, and I have a Powerbeam Pro with ant+. I’m assuming the trainerroad app won’t be able to work with the powerbeam pro unless the phone has built in ant+? I might have to end up buying a kickr snap….
I’m not sure yet, but I believe you’ll be able to use a variety of ANT+ dongles with Android. So you should be able to use your current Android phone with an ANT+ dongle. I can’t promise that until closer to launch though.
Five requests:
– improve the power/cadence equation (i.e. adjust faster to changes in cadence.) Ideally, leveraging per-rider historical data from recent efforts (“Hmmm… Rider seems to be doing 240W @ 95 rpm, but does 300W @ 80 rpm. Let’s predict that and adjust ERG accordingly.)
– display HR Zone (blue/green/yellow/red, whatever) against a per-rider profile. Garmin shows %HRR / %HRMax / HRZone, and TR should, too. (Yes, we’re training with power, not HR, but better metric alignment with head units is a good thing. No-one looks at raw HR on their Garmin while riding.)
– add a “Discard” option for ending a ride. Sometimes you just bring up a ride to see that all the gear and gauges are working as expected, while producing no meaningful data / effort / workout to record.
– allow a cadence target and show the under/over bar against the target (e.g. Rubber Glove w/90 rpm targets, or custom high/low cadence drills.)
– allow tweaking effort (90%/110%) using a presentation remote (i.e. custom key mapping.)
One question: are you planning to release the app also via Mac App Store? And related: do you see offering subscriptions via in-app purchase (a la Strava Premium on iOS)?
Please don’t add a discard option. The discard option on my Edge 810 is one of least favorite features. I’d rather a device always saved my workout and allowed me to delete it later! I have to be so careful when I end a ride, I’m always worried that I’m going to fat finger it and lose it all!
Thanks for the suggestions AC :). A discard option is built in this next update.
I don’t think we’ll release the app in the Mac App store. That makes us go through the apple approval process every time we want to update which can seriously hamstring us.
We don’t plan on offering subscriptions via in-app purchases either. Apple takes 30% right off the top of that subscription and I don’t think we’d have a good way to restrict access on our desktop app for those who signed up via iOS.
Hey Alex, we’ve built in a discard option but it has another layer of “Are you sure you want to Discard this ride?”. So even if you click wrong you have another chance immediately afterwards.
Thanks for letting me know. I’ll probably be able to avoid hitting the wrong button twice! I always thought the existing “save all activities” approach was well thought out :)
The suggestion to improve power/cadence equation has been boggling my mind enough I have to ask if anyone understands what the suggestion is and can explain it to me!
I cannot seem to grasp a tightly coupled relationship between cadence and power for almost any sense of riding. Perhaps if a gear selection and trainer curve is known, then cadence would somehow correlate to power (through the gear ratio, tire size and eventually trainer speed to trainer power curve), but otherwise I can’t see how knowing cadence ever helps with gleaning data into power output.
Sure if it is a power meter knowing cadence and torque is needed for calculating power, but that isn’t something TR is doing or cares about when a power meter is in play?
Am I silly and confused?
I don’t really have any other accessories to use wirelessly, but when I do use my laptop it is out of reach and a “remote” to adjust intensity is interesting.
Re: Cadence/Power/KICKR/TR, see this thread.
Everybody i know is looking at raw HR-data!?
You need exact numbers while racing!
an bo, we don’t need a discard option! There is simply too much risk for loosing a workout!
full ack! way better from the interaction-design persoective!!
I think Ray’s idea for an Apple TV app is fantastic. I’m already using my Apple TV and Airplay to see the workout, and taking the laptop or iOS device out of the equation entirely would be great. But I think your reply above about the Mac App store is pretty telling. But I can dream.
I don’t think the lack of a Mac App Store app is in any way linked to a potential Apple TV app. OS X has always had a “traditional” app install path, so there’s no need to offer a Mac App Store version. As TrainerRoad doesn’t support iCloud documents etc., the app works just as fine as a standalone install.
The main issues I’d see with an Apple TV TrainerRoad app are embedded video playback (ironically) and ANT+ sensor support. At least with iOS you can manage the on-device video library via iTunes, but on an Apple TV you’d have to use Home Sharing or iCloud instead. And I don’t think you can just plug in an ANT+ USB stick on an Apple TV via the USB-C dongle and just expect it to work w/o some MFi magic.
Still, I’m looking forward to running TrainerRoad natively on an Apple TV w/tvOS :)
Is there an option on the new desktop version to amend the colours on the graph? I would really like to remove the blue blocks so that’s it’s easier to see the yellow line.
There won’t be at first launch. I think a “high contrast” mode would be good for vision impaired people.
The new shades of blue and yellow in the desktop app are a little different now too. It technically has more visual contrast than the current desktop app.
The changes are looking rally nice! Looking forward to trying the new version (and the Android version later too).
I saw you mentioned Best Bike Split for creating a workout from a GPX file: Do you have any plans to implement this directly into the new program? If I want to ride a GPX file currently, I have to use CycleOps Virtual Training. I’d rather keep all of my workouts in one place, and I love the ease of TrainerRoad. Perhaps this is something you will add further down the line?
Yes, we plan on doing this in our own app. It’s part of our longer term super secret roadmap ;).
Thanks for the nice words about the app!
Hi Nate,
I might have misunderstood, but the beta is for Windows? If that is the case, will there be a beta/launch for OS X users as well (from Ray’s pictures it looks like you are showing of the new desktop version on a MacBook Pro?) ?
Alex
Yes, beta is for Windows only. As soon as we get Windows out you’ll see a beta for Mac and Android soon after that.
That is a Macbook Pro in the screenshots. It’s using Parallels to run Windows 10. Sorry about that, I can see how that can be confusing :).
Hi Nate, would there be any chance of a release that would work on Linux?
Hey Lee. Right now we have no plans on doing a linux version of TrainerRoad. We just don’t think there’s the market share to make an app that runs on Linux. Sorry :(.
This is great I use them for the last 2 years I guess as a complement to the normal bike
When is the new release planned is there a date , haven’t seen it
We’re aiming for two Mondays from now. Of course in software, last minute bugs could prevent us from hitting that date on the nose.
Nate,
Is there any chance in the nearish future TrainerRoad will auto upload to Garmin Connect?
Cheers!
Sorry for the late reply, I missed this one.
I’d love to auto upload workouts to Garmin Connect. The problem is they don’t have an offcial API.
I know it’s technically possible to impersonate a user and push the workouts, but I’m afraid that if we push a high number of workouts Garmin might shut us off.
I believe Ray mentioned that something like that has happened before.
I that were to happen, we’d have a ton of pissed off users and no way to make it right :(.
The secondary concern I have is storing someone’s Garmin Connect user/pass locally. Although we can do all the best practices to keep someone’s data safe, it’s never best practice to store external website’s username/passwords in your database.
Although we could make it as secure as possible, it just makes us feel weird.
The best situation would be if Garmin opened an oAuth based API where we could push workouts. It looks like they don’t want to allow that though :(.
Ray might have more info. If we could get assurances that we won’t get cut off from Garmin Connect I’d put it on the roadmap to implement.
Indeed, Nate is pretty much spot on. In a nutshell Garmin charges $5,000 to access the backend API (that’s more secure). Some companies pay that (i.e. TrainingPeaks, Sport Tracks, Nike, etc…). Or, if not pay it, are waived. And then others circumvent it (i.e. Wahoo, Tapiriik, and many other mobile apps).
Now interestingly, I saw in the ANT+ Newsletter that if one is going to the ANT+ Symposium next week and happens to attend the Connect IQ session (about 1hr long), then they’ll get the $5K fee waived.
I suppose paying the Symposium fee ($749) + travel is probably significantly cheaper than paying the $5K fee. Plus, you get to hear me speak, and the bacon that’s included at breakfast is usually pretty good. :)
Ray, the $5000 fee is only to pull workouts from Garmin into TR, correct? I thought we couldn’t push workouts into Garmin Connect. If that’s the case, we’ll gladly pay the 5k!
Lorentz (our CTO) is going to the ANT+ Symposium next week :). I’m going to be out of town or else I’d go too.
Great to hear about the Connect IQ session.
Hmm, good point, it is more of a pull (reception) than a push. Trying to think of anyone is pushing into it….
That said, the right folks over that specific function will be at that session – so they’re definitely the ones to lay out your thoughts to.
Ray / Nate
Thanks for taking the time to reply. I guess my other option (and I haven’t used it yet) is to have my 810 on at the same time to pick up the speed/cadence/HR of the work out? and use that to upload to Garmin (which will then feed to Strava, Sporttracks and Fetcheveryone)
Does that make sense?
Cheers
Dave
That’s what I do, just make sure you enable Trainer Relay so that your power gets broadcast to your Edge as well to complete the data set.
That’s what I do too.
I use my Garmin 910XT to record the cadence / speed / distance / HR, then upload to Garmin. This then autosyncs to Strava. Wife and kid do same with their Fenix 3’s.
I miss out on the virtual power data that you get when using TR to sync to Strava but it was too much hassle to then put that data into Garmin, so I turned it off.
like many others I use Garmin Connect to dump all my data, then auto sync off to Strava (for social) and Sporttracks (for analysis).
A direct sync / upload to Garmin would be cool. I bet the percentage of TR users that use a Garmin device and Connect are relatively high.
Thanks lee – didn’t know I could do that – so I can get my virtual power relayed back to my Garmin? Which then uploads as above.
….off to see if it works on my 910xt – fantastic if so, thanks for the heads up.
Sorry for the late reply, but yes, TrainerRelay will send VP data to your 910xt.
Thanks Nate, works a treat & nice to see the VP graph when uploaded to GC.
Shame the virtual relay is not a feature of the iPad app for my Mrs…..maybe a future upgrade?
you should try https://tapiriik.com
shame about linux. but looking forward to the native windows app.
I am from Belarus. I am use TR about 3 years. All workout with instructions is problem for me – I can’t read so fast and hard ride in same time. Any plans for different languages? Or export instructions for reading before ?
Hey Andrey. I’m sorry, we don’t have any near term plans to go multi lingual for our workout text. We’d like to do it some day, but it’s not on our roadmap at the moment.
Nate, since Windows beta is written in WPF, its not really native code. Do you have plan to port it to universal windows app? Your Wpf code is probably already 95% recyclable to universal app platform.
There’s no plans on going to a Windows universal app right now. Sorry :(
Any update on the release date Nath?
Right now our beta release for Windows is scheduled for Tuesday of this week. Of course, critical bugs could change that date.
Hi Nate
Any further update on this?
Any ideas on a beta release date for Android?
Winter is coming and I have to pick-up a solution for the upcoming long Canadian winter training.
Hi Nate, Hi Ray
Any chance this new version will work with other bluetooth 4.0 adapters other than the Bled112?
thanks!
Yes, we’re working on that. First release will require the bled112 but we’re going to support native Bluetooth on Windows 8 and 10.
Older versions of Windows will still require the bled112.
We found a critical device layer bug just before launch and we’ve been fixing it. We have another round of final testing today; if that goes well the first beta will be at and advertised at our Facebook page at link to trainerroad.com
That link doesn’t work… looking forward to new version.. hopefully no more AIR apps :)
The beta is out but it doesn’t recognise the Garmin ANT+ dongle. I’ve tried with 2 different PCs and no luck…works fine with the non beta version of trainerroad. Anyone else with the same problem?
Triple check that the older TR isn’t running in the background. The ANT+ stick can only take one concurrent connection to it, so if something else (older TR, Garmin ANT Agent, Garmin Express, etc…) then that’s a problem.
Though, the fact that you’ve tried it on two machines is odd…
Thanks Ray. Definitely weird, as I’ve checked that garmin ANT agent would recognise the dongle, then I’ve uninstalled the gym in agent, went into task manager and made sure that no other process was using the ant dongle, went into the beta version of trainerroad and still nothing. When I launch the stable version of trainerroad and it would just work straight away…ive even tried on a mac with parallels, and it’s the same problem. I’ve already faffed enough with this, giving up! :)
Hey redheb, you must have been checking our beta URL! We didnt even announce that it was live :). We turned it on to do some internal testing and found that a library wasn’t deployed correct; thus ANT didn’t work.
The good news is that’s been fixed! To get the update simply open your app. After about 10-30 seconds (depending on your internet speed) there should be a notice that says “update available”. Just restart the app and it will be installed :).
You can also download the beta (or anyone else who wants to try it) here: link to trainerroad.com
We’re not feature complete on this beta, there’s a list of things that isn’t in the beta yet on the beta install page. And as always, if you run into any problems let us know at support@trainerroad.com.
Happy Training!
Great! Thx Nate.
Hi Nate,
any time frame when a Beta for Mac will be available?
Thanks!
We’re deep into OSX development now. I don’t have a timeline but we’re excited about our development pace.
Hey, been using TR for about a month now with and without sufferfest vids (since I got my kickr) and I’ve got to say it’s the best bit of cycling kit I own.
One thing that would be cool is if in workout creator it would be possible to create an “unlimited” interval where you are not limited by your power target (instead of mid workout reaching for the M button to switch from ERG to resistance) and back again. This would be good for sufferfest workouts especially when there is a bridge/attack type segment where it would be good to see how much you can go into the red and recover.
Thanks DC and Nate!
Damo: have you tried setting the percentage of FTP higher? I mean, if you can set it to 110% or 120% and survive, I’d assume your FTP is wrong :)
Hey, yeah I do that sometimes. I find it telling to be able to unload on the final sprint especially in when you are monitoring your progress over a 10 week program etc. Higher numbers mean you’re getting to the line with more in the tank etc…. :)
Anyone have a promo code for trainer road yearly subscription?
are you looking for a year’s worth of free trainer road?
Someone is giving out monthly free
Ha! Free? Well sure if you’re offering hahaha. Just didn’t know if there was an X% off discount code floating around for a full year as Im about to join
Has anyone gotten this working for the older Cycleops 400 machines? It works on their older application.
Will devicerelay work with iOS? I’m putting together the following setup:
kurt kinetic trainer with inride power meter bluetooth smart
ipad pro with lighting to 30 pin adapter and wahoo ANT+
garmin speed/cadence ant+
garmin edge 810
idea is to receive to use the inride power on trainerroad on ios to follow workouts and have that power data broadcast from the ipad to the garmin edge 810 to seamlessly upload to garmin connect afterwards.
Device relay doesn’t work on iOS, sorry :(.
Hi Nate, Hi Ray,
Any update on Android app progress? I signed up for “updates” the day Ray released this post, and yet 8 months on and there hasnt been a single update as far as I can tell. It’s your business of course, and if you’ve pushed Android development into the long grass that’s your decision, but could you at least let us TR subscribers know that? A bit more transparency on status would really be appreciated, even if it’s not the news I necessarily want.
Regards
Hi Steve – everyone,
Really sorry for the delay on Android guys, and also for the absence of recent updates! We’re extremely excited to get everyone enjoying TR on their Android devices, but we’re still working diligently to make sure everyone will be able to do so reliably. While we are getting closer, as many of you know, the nature of software development can spark some unforeseen road blocks. And while the complete revamping/redesign of the Windows app took a little longer than expected, it had to be implemented in a way that’s up to the TR standard. We plan to deliver the same level standard to Android and Mac as well. These are the primary focuses of the team, and while it’s taken longer than anticipated, we’re confident it’ll be everything that everyone’s been waiting for – and then some. :-)
Thanks again for everyone’s patience. We’ll be sure to keep everyone up-to-speed!
Thanks Nick.
I fully understand wanting to get an app out that is worthy of the TR brand and up to the standards you have set yourself. I would just suggest that the type of update you have provided above should be something you push around to the wider TR subscriber base who have registered Android interest. Whilst Ray’s site is great, I think most would expect updates to be coming direct from source using the mailing list we signed up to, rather than having to resort to checking here!
Looking forward to it finally hitting Google Play. Hopefully not too much longer… ;)
Thanks for your — and everyone else’s — understanding here man.
I’ve passed your feedback along to the rest of the team. The plan is to have a beta out for everyone by Interbike. In any case, I think one of the main hang-ups on a widespread email is just getting a clear idea of our time-line.
Hopefully not much longer indeed my friend. :-)
Hi,
Just bougth a Tacx Neo and I wanted to try Trainerroad.
Unfortunately the promo code “DCR10MHD” from DC Rainmaker does not work anymore :-(
Too bad that was a good incentive.
Congrats on the new toy!
Regarding the promo code: You can occasionally find them posted in various cycling forums as well. That said, we have a 100% money-back guarantee! If you don’t absolutely love us in your first 30 days, we’ll refund you all your money no questions asked. :) We’ll be looking forward to getting some hard-earned training in with you very soon. Happy training!
From the Sept 17, 2015 comment: “We’re talking to Tacx about this today. I’m fairly confident that we’ll be able to control Tacx trainers over Bluetooth this winter. No promises, but I think it can happen. Right now the ball is in their court, but they have expressed interest.”
Any chance this happened? I guess I’ll try it out in a couple days on my iPad Air 2 when I’m next able to use my Tacx Neo, but if not that means I’ll need a Wahoo ANT+ key and Apple Lightining to 30-pin adapter? That’s over $100 here in Canada! Plus I’ve heard the key doesn’t have much range. Unlike on a desktop where you can just run a USB extension to an ANT+ stick, the longest Apple extension with the correct ends is under 8 inches.
I’d rather not spend >$100 to then find out the key has spotty connection with my Neo, but I also don’t have a good place for my desktop where I ride my Neo…
My winter would be complete with TR on my iPad Air 2 connected to my Neo by Bluetooth.
Hi (from Canada also)
I am using a Tacx Neo with an Ipad Air 2 and the Wahoo ANT+ key/Apple Lightining to 30-pin adapter and it works perfectly (the Ipad is on a stand in the front of the bike, approximately 10-15 inches away from the handlebar )
You just have to make sure that the Ipad has enough battery because with the use of the Wahoo ANT+ key you cannot charge the Ipad at the same time (and this would be definitely a big advantage if Trainerroad would use the bluetooth connection with the Tacx Neo)
Thanks Tony! Guess it’s time to buy another addition to the setup, TR staff replied (equally quickly!) that they haven’t been able to get the proper communication protocols integrated into TrainerRoad for Tacx over Bluetooth yet.
Can’t wait to start proper winter training for the first time!